شرح درس مساحة الدائرة للصف السادس

درس مساحة الدائرة للصف السادس من الدروس المعقدة بالنسبة للطلاب، حيث أن الدائرة تعتبر شكل من الأشكال الهندسية مغلق، ويشبه المنحنى الهندسي الذي يتكون من خط مائل ثنائي الأبعاد، والخط الذي يوجد به يتكون من عدد لا نهائي من النقاط، وكل نقطة تبعد مساحة محددة وثابتة عن مركز الدائرة، وسوف نتناول شرح مساحة الدائرة خلال هذا المقال.

مساحة الدائرة

مساحة الدائرة تعني المساحة التي تمتلكها الدائرة على سطح غير منحني ويكون مستوي أو في مستوى ثنائي الأبعاد، حيث يعتمد مساحتها على نصف القطر بشكل رئيسي، ويمكن حساب المساحة من خلال القوانين التالية:

• مساحة الدائرة= *π(ق/2) ².
• مساحة الدائرة= نصف القطر² π ×.
• حيث أن π: قيمة عددية ثابتة مُساوية 3,14.
• ق: تُمثل قُطر الدائرة.
• لابد من توافر ثلاثة أشياء لحساب المساحة، ألا وهم ط والقطر ونصف القطر.
• ق تعتبر اختصار لكلمة قطر، ونق اختصار لكلمة نصف القطر.

بعض التعريفات الخاصة بالدائرة

من خلال السطور التالية سوف نقدم لكم بعض التعريفات الخاصة الدائرة لكي تتمكن من حل المسائل بسهولة وهي الآتي:

• نِصف القُطر (نق): هي المسافة بين مركز الدائرة وأي نقطة على منحنى الدائرة.
• القُطر (ق): هو الخط المستقيم الواصل بين أي نقطتين على منحنى الدائرة، أو يمكن اعتباره بأنه الخط الذي يقسم الدائرة إلى نصفين.
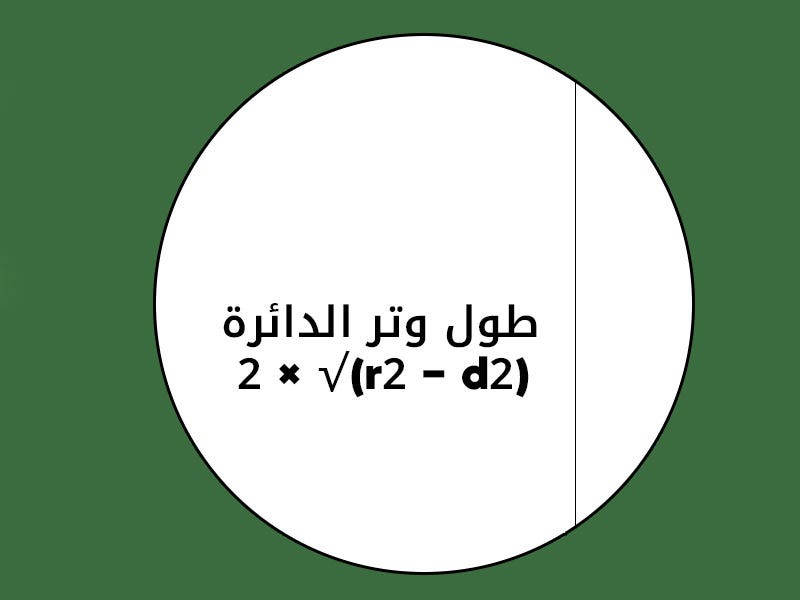
• وتر الدائرة: هو الخط المستقيم الذي يمر بأي نقطتين على منحنى الدائرة ولكن ليس من الضروري أن يمر بمركز الدائرة، لذلك يوجد لكل قطر وتر وليس العكس.
• العدد ط: ما هو إلا عبارة عن رقم له قيمة ثابتة ألا وهي قيمته تُساوي 22/7 أو 3,14.

محيط الدائرة

من خلال السطور التالية سوف نتعرف على طرق حساب محيط الدائرة والتي تتمثل في الآتي:

• المحيط يعني طول الخط المحيط بجميع حدود الدائرة وتقال بالمتر أو السنتيمتر وهكذا.
• محيط الدائرة= حاصل ضرب القطر في باي.
• محيط الدائرة= حاصل ضرب 2 في ثابت الدائرة ط في نصف القطر.
• يمكن حساب محيط نصف الدائرة باستخدام هذا القانون: *πنصف القطر
• يوجد ثلاثة عناصر أساسية لا غنى عنهم لحساب المحيط ألا وهو القطر او نصف القصر و ط.

حِساب مساحة الدائرة بدلالة المُحيط

من خلال السطور التالية سوف نتحدث عن طرق حساب المساحة عند توافر المحيط، والتي تتمثل في الخطوات التالية:

• احسب نصف القطر عن طريق كتابة قانون المحيط.
• قم بالتعويض عن قيمة نصف القطر لإيجاد المساحة المطلوبة.
• وبذلك يكون قانون المساحة بدلالة المحيط كالآتي: مساحة الدائرة= مُحيط الدائرة² / (4×π)، مربع محيط الدائرة على باي في 4.

حِساب مُحيط الدائرة بدلالة المساحة

يمكن حساب محيط الدائرة من خلال توافر المساحة ويتم ذلك باتباع الآتي:

• قم بتعويض قيمة المساحة باستخدام قانون المساحة.
• احسب نصف القطر باستخدام قانون المساحة.
• عوض عن قيمة نصف القطر في قانون المحيط لإيجاد قيمة المحيط.
• يمكن حساب المحيط بطريقة مباشرة عند وجود المساحة من خلال القانون التالي: محيط الدائرة = (مساحة الدائرة (4 × π × حاصل ضرب المساحة في ثابت الدائرة ط في 4.

في الختام وصلنا لنهاية المقال الذي قدمنا فيه شرح الدائرة وكذلك المساحة والمحيط وكذلك طرق حساب المساحة بدلالة المحيط والعكس كما تحدثنا عن التعريفات الخاصة بالدائرة والتي تمكن الطالب بفهم الدائرة بشكل صحيح، حيث أن الدائرة واحدة من الأشكال الهندسية الهامة في الرياضيات.